插入排序 | 破晓狂客

(一) 算法描述

将n个元素的数列分为已有序和无序两个部分，每次处理就是将无序数列的第一个元素与有序数列的元素从后往前逐个进行比较，找出插入位置，将该元素插入到有序数列的合适位置中。

(二) 算法分析

最差时间复杂度：\(O(n^2)\)

最好时间复杂度：\(O(n)\)

平均时间复杂度：\(O(n^2)\)

空间复杂度：　　\(O(1)\)

稳定性：　　　　稳定

(三) 算法伪码

INSERTION-SORT(A)
for j=2 to A.length
	key = A[j]
	//Insert A[j] into the sorted sequence A[1..j-1].
	i = j-1
	
	while i>0 and A[i]>key
		
		A[i+1] = A[i]
		i = i-1
	A[i+1] = key

(四) 图解样例

下图每次迭代中，黑色的长方形保存取自A[j]的关键字，测试中将它与其左边的加阴影的c长方形中的值进行比较，加阴影的箭头指出数组值向右移动一个位置，黑色的箭头指出关键字被移到的地方，最终排好数组。

图解样例

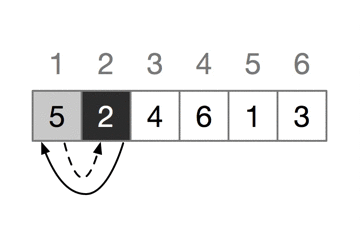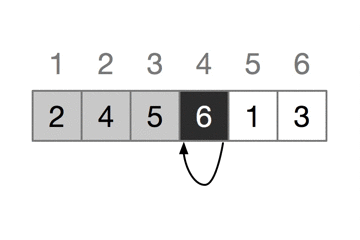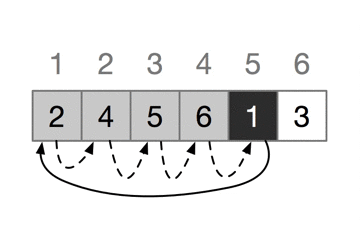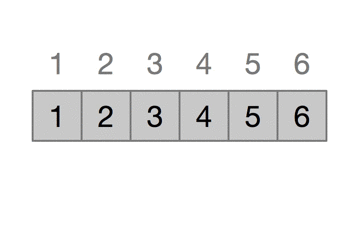
(五) 算法步骤

当前需要排序的元素(A[i])，跟已经排序好的最后一个元素比较(A[i-1])，如果满足条件继续执行后面的程序，否则循环到下一个要排序的元素；

缓存当前要排序的元素的值，以便找到正确的位置进行插入；

排序的元素跟已经排序号的元素比较，比它大的向后移动(升序)；

要排序的元素，插入到正确的位置。

(六) java实现

public class InsertSort{

    /**
     * 排序函数
     *
     * @param data  输入数组
     * @param order 排序方式：
     *              true为升序
     *              false为降序
     * @return
     */
    public int[] sort(int[] data, boolean order){

        if(data.length == 0){
            throw new NullPointerException("数组为空");
        }

        if(data.length == 1){
            return data;
        }

        for(int i = 1; i<data.length; i++){
            int key = data[i];
            int j = i - 1;
            if(order){
                while(j>=0 && key<data[j]){
                    data[j+1] = data[j];
                    j--;
                }
            }else{
                while(j>=0 && key>data[j]){
                    data[j+1] = data[j];
                    j--;
                }
            }

            data[j+1] = key;
        }

        return data;
    }
}

(七) python实现

class InsertSort(object):

    """插入排序类"""
    def __init__(self):
        super(InsertSort, self).__init__()

    def sort(self, datas, order):
        """对传入的数值数组datas进行插入排序.

          Args:
            datas: 待排序数值数组 e.g. [12, 3, 24, 11, 34, 33, 42, 9, 4]
            order: 排序顺序 e.g. True为升序， False为降序

          Returns:
            datas: 排好序的数值数组.
          """

        for i in range(1, len(datas)):
            j = i-1
            key = datas[i]
            if order:
                while j >= 0 and key < datas[j]:
                    datas[j+1] = datas[j]
                    j -= 1
            else:
                while j >= 0 and key > datas[j]:
                    datas[j+1] = datas[j]
                    j -= 1
            datas[j+1] = key
        return datas


def main():

    data = [12, 3, 24, 11, 34, 33, 42, 9, 4]
    print data
    order = True
    insert_sort = InsertSort()
    result = insert_sort.sort(data, order)
    print result


if __name__ == '__main__':
    main()

(八) 算法缺点与优化

1. 缺点

比较次数不一定，比较次数越少，插入点后的数据移动越多，特别是当数据总量庞大的时候。

2. 优化

直接插入排序每次往前插入时，是按顺序依次往前找，可在这里进行优化，以下为常见的两种优化算法：

折半插入排序算法

希尔排序算法

(九) 总结

插入排序是最简单的排序算法之一，当数据基本有序时，采用插入排序可以明显减少数据交换和数据移动次数，进而提升排序效率。

参考博客

插入排序及优化

排序算法之二分法（折半）插入排序算法

排序算法总结